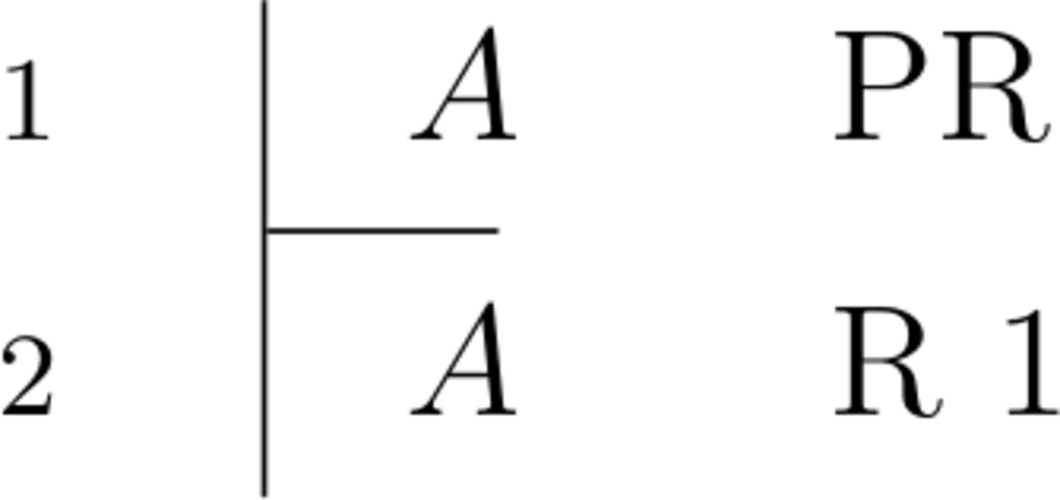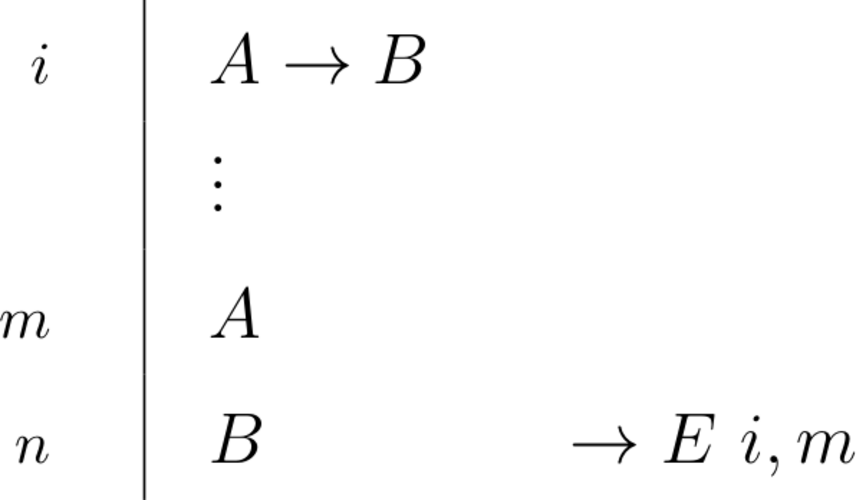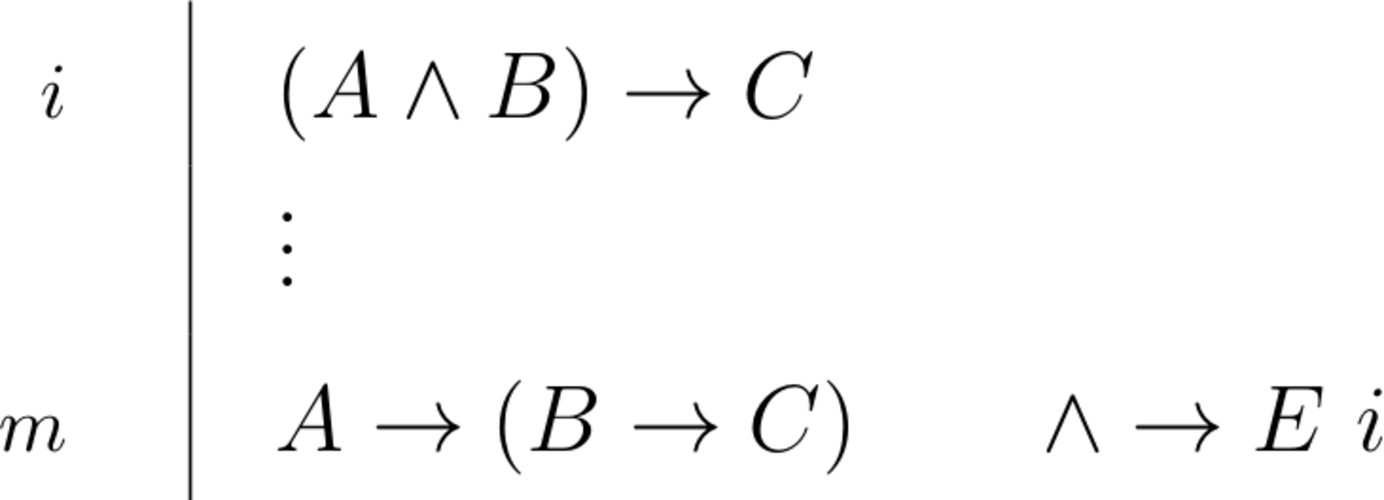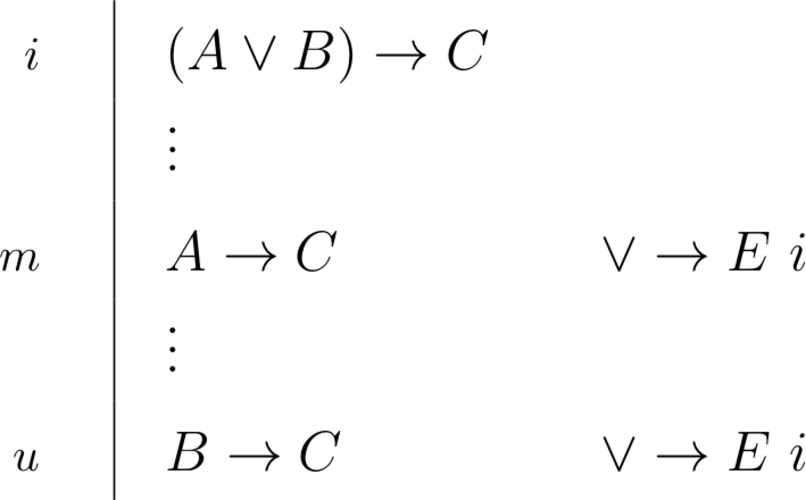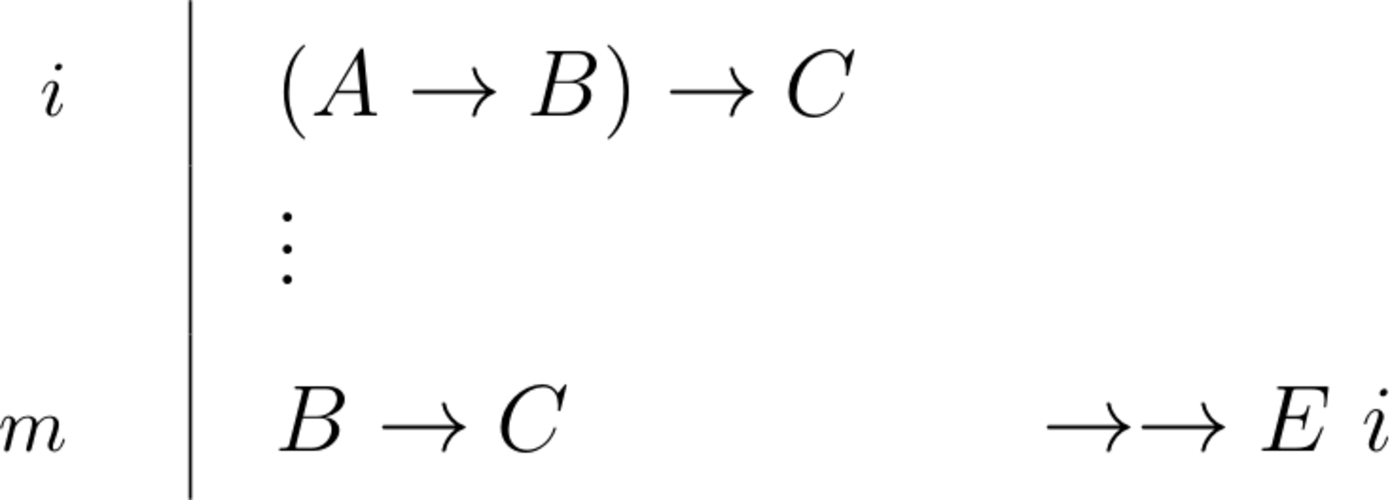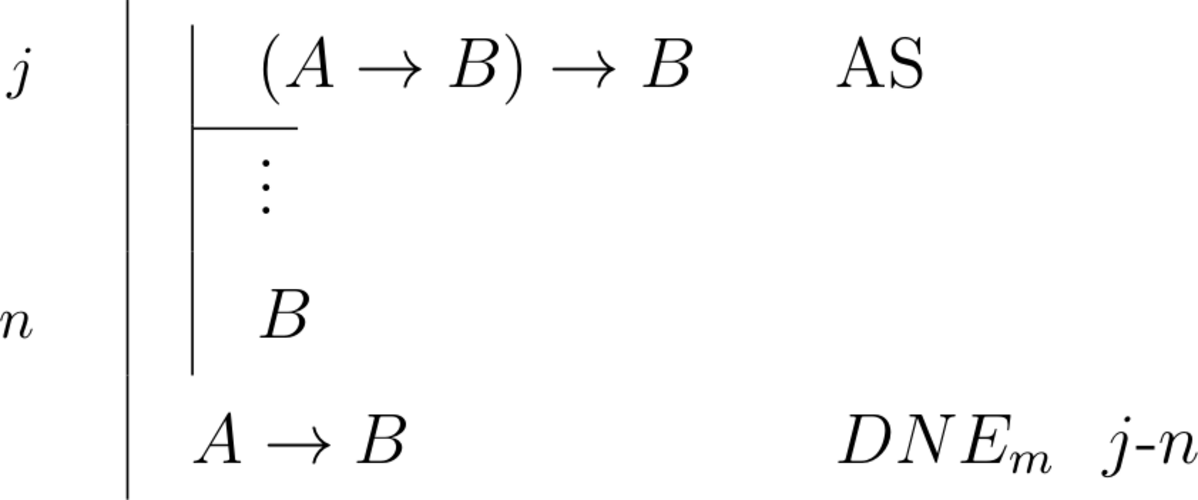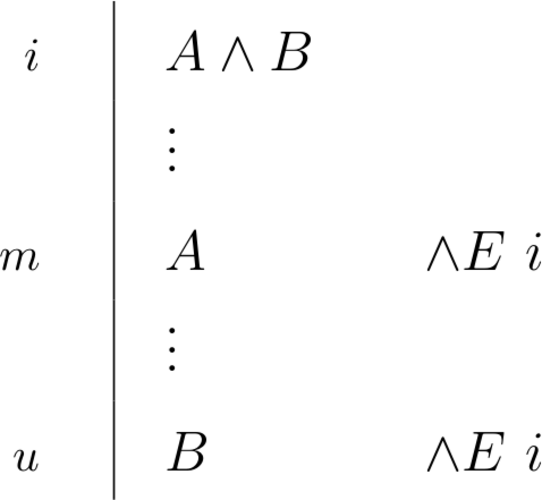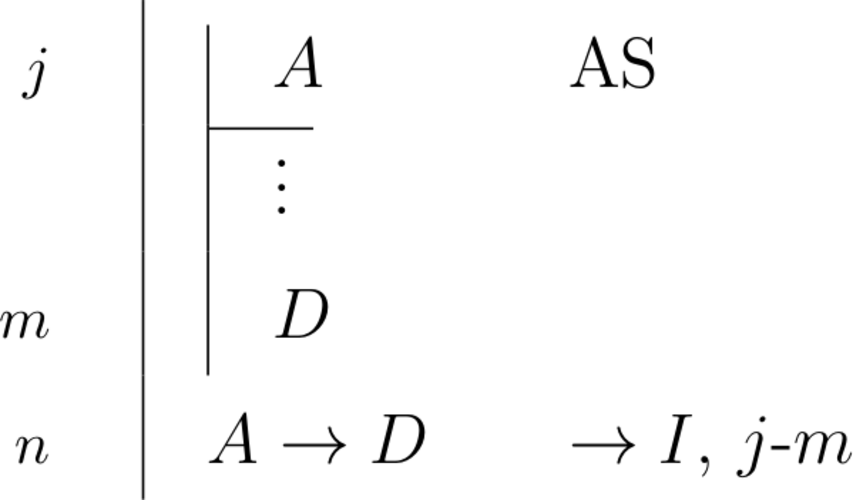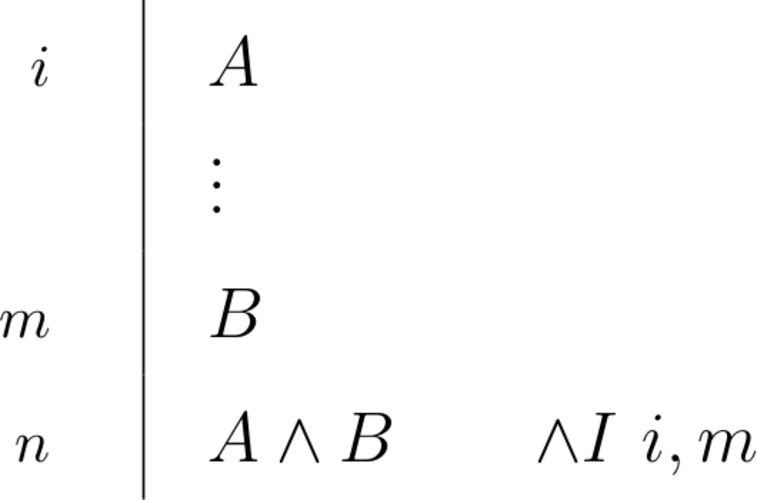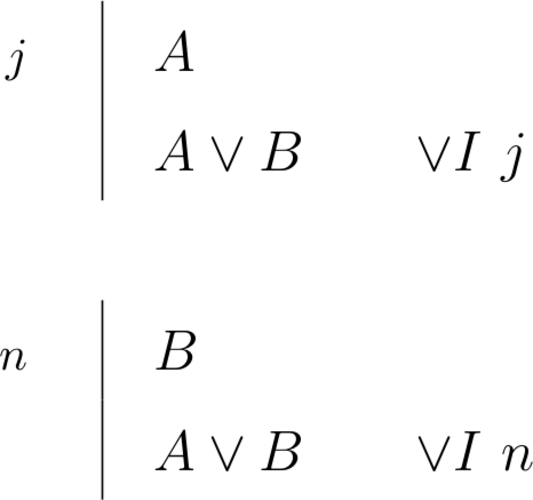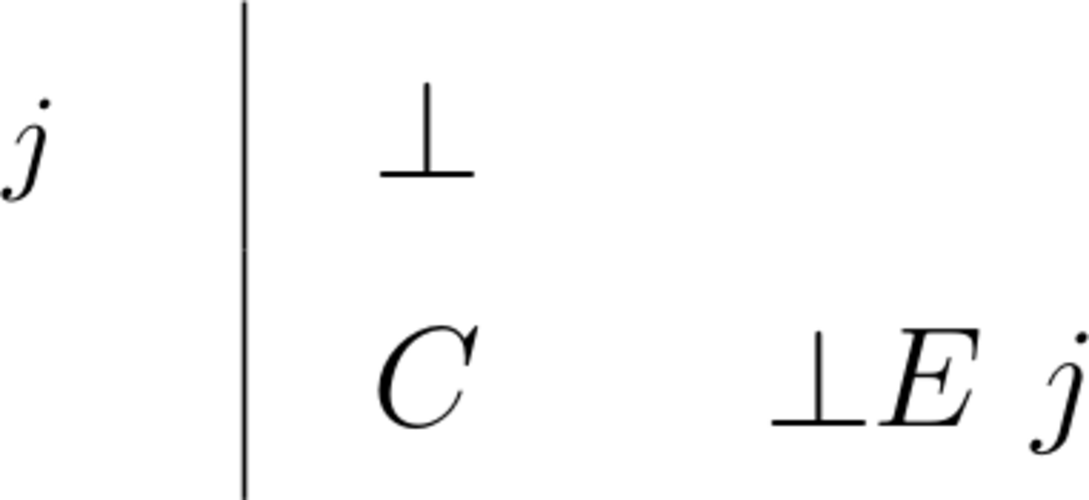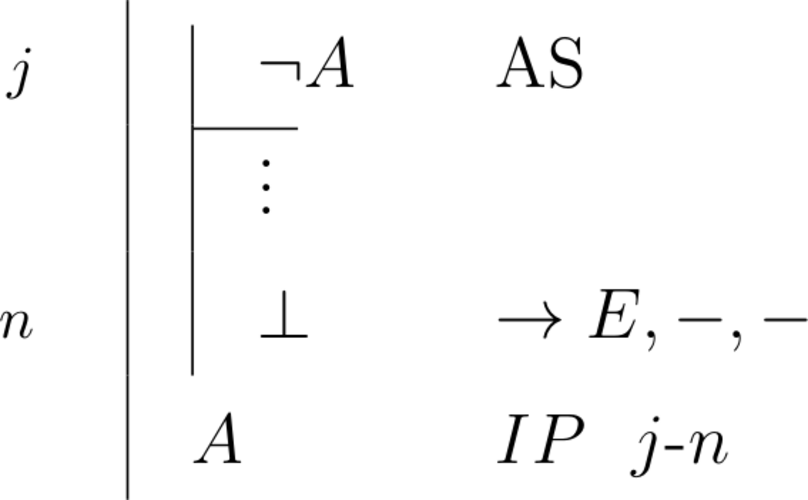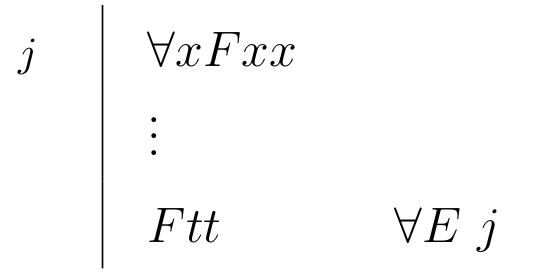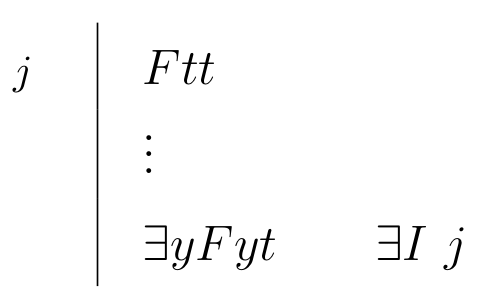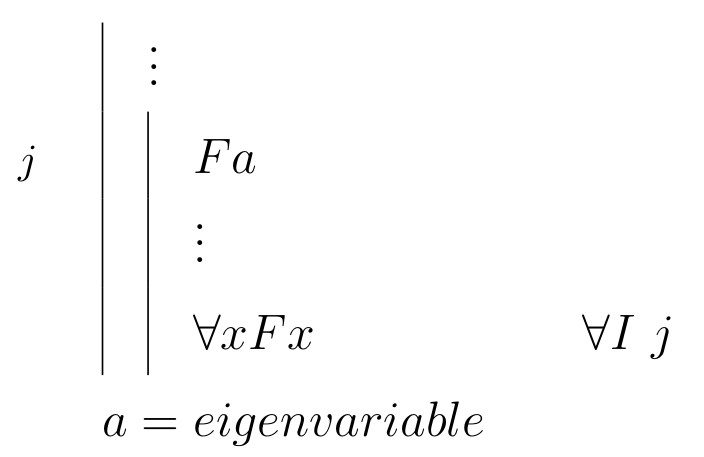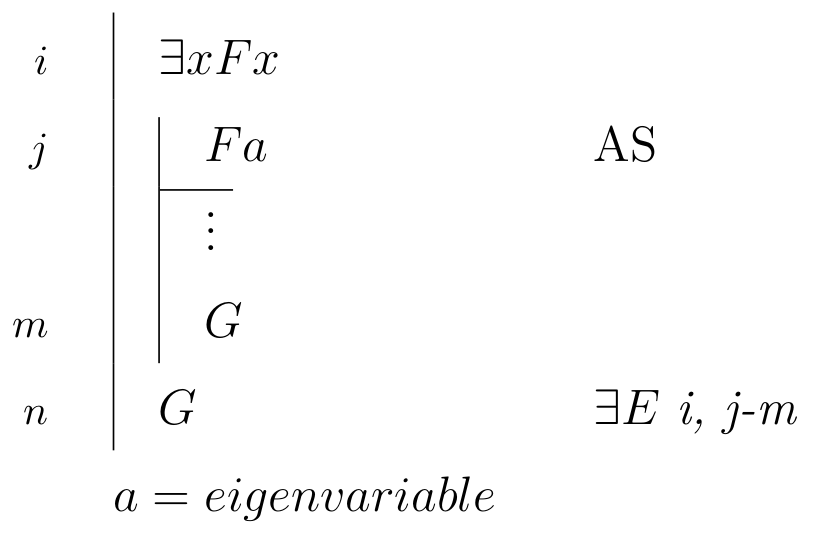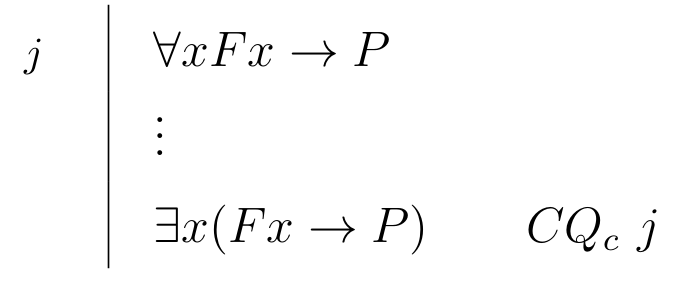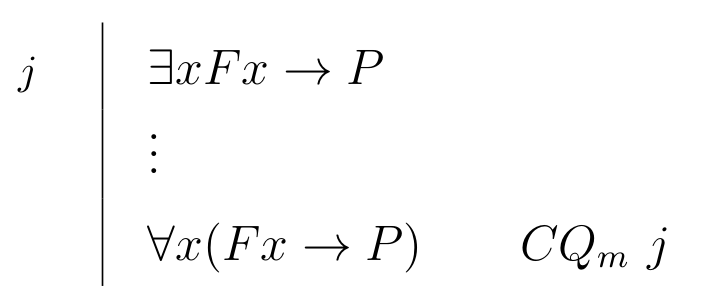SWI-Tinker for G4-mic F.O.L. Prover

G4-mic is an automated prover for minimal, intuitionistic and classical First Order Logic written in SWI-Prolog. G4-mic is mainly based on rules for direct syntactic deduction which are the rules of sequent calculus G4 and their translation in natural deduction (in tree style and Fitch style).

(Note that G4 was not classical: when it was defined by Dyckhoff [1] (who called it LJT to stress the terminating property which was lacking in sequent calculus LJ), G4 was not classical, but intuitionistic. By adding rules IP and CQ_c, this F.O.L. prover becomes classical, while remaining single-conclusion.)

1. G4-mic provides \(\LaTeX\) proofs in these three formats, which you can share via URL addresses (like with Wolfgang Schwartz’s Tree Proof Generator). For example, the solution to exercise i given by Lepage [2, p. 146] finds another proof in minimal logic via this link.
2. Note that, if your formula is provable, G4-mic tells you the logic level that is at least required to prove it, i.e. either minimal, intuitionistic or classical logic.

• The code of the proof engine has been inspired by Jens Otten’s leanseq.
• The smart system for printing labels and reference lines in Fitch proofs has been invented by B., a Prolog expert who usually dislikes seeing his name quoted.
• On this basis, the driver and the printers have been written with the help of A.I., mainly Claude, without which I would not have succeeded in making this work.
• Finally, the web page dedicated to G4-mic is also a SWI-Tinker that you can use to test your Prolog programs online, with other SWI-Prolog provers in the Demos library, thanks to the generous work of Jan Wielemaker given to people for free. My warmest thanks to Jens, B., Jan and Claude, and my apologies to those I have forgotten.

The source code of G4-mic is on Github under the GPL v3 license.

Rules for Sequent Calculus G4	Natural Deduction Rules in Tree Style	Natural Deduction Rules in Flag Style
\begin{prooftree}\AxiomC{}\RightLabel{\scriptsize{$Ax.$}}\UnaryInfC{$A, \Gamma \vdash A$} \end{prooftree}	\begin{prooftree}\AxiomC{$A$}\RightLabel{\scriptsize{$R$}}\UnaryInfC{$A$} \end{prooftree}
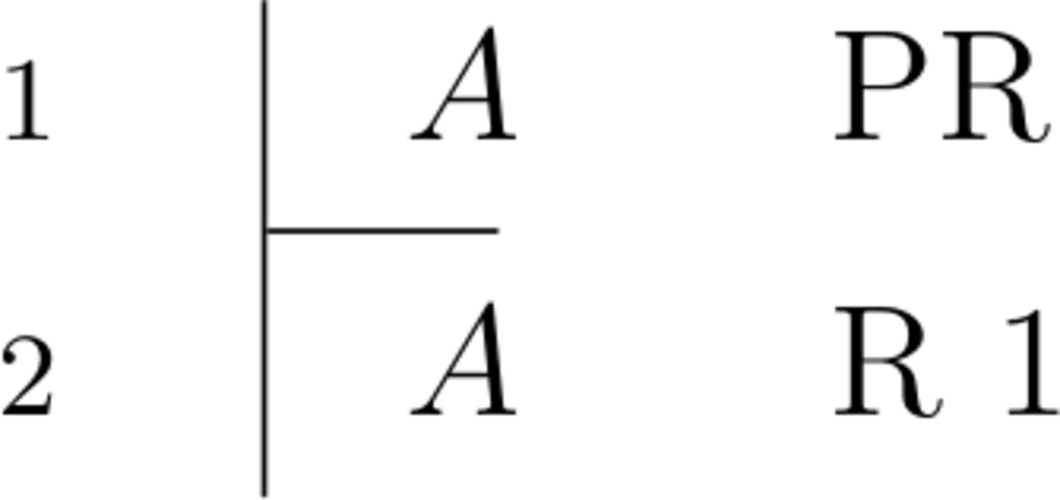\begin{prooftree}\AxiomC{$A, B, \Gamma \vdash C$} \RightLabel{\(\scriptsize{L0\to}\)} \UnaryInfC{$A \to B, A, \Gamma \vdash C$}\end{prooftree}	\begin{prooftree}\AxiomC{$A \to B$} \AxiomC{$A$} \RightLabel{\scriptsize{$\to E$}}\BinaryInfC{$B$}\end{prooftree}
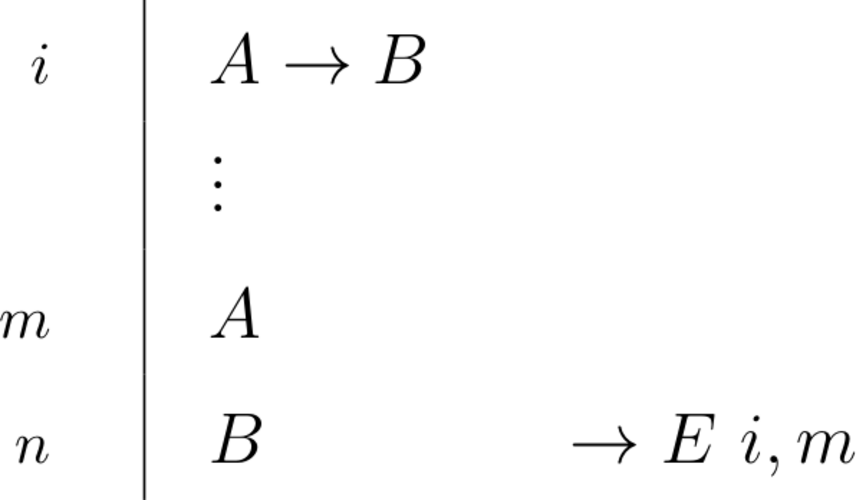\begin{prooftree}\AxiomC{$A \to (B \to C), \Gamma \vdash D$}\RightLabel{\(\scriptsize{L\land\to}\)}\UnaryInfC{$(A \land B) \to C,\Gamma \vdash D$}\end{prooftree}	\begin{prooftree}\AxiomC{$(A \land B) \to C$}\RightLabel{\scriptsize{$\land\to E$}}\UnaryInfC{$A \to (B \to C)$}\end{prooftree}
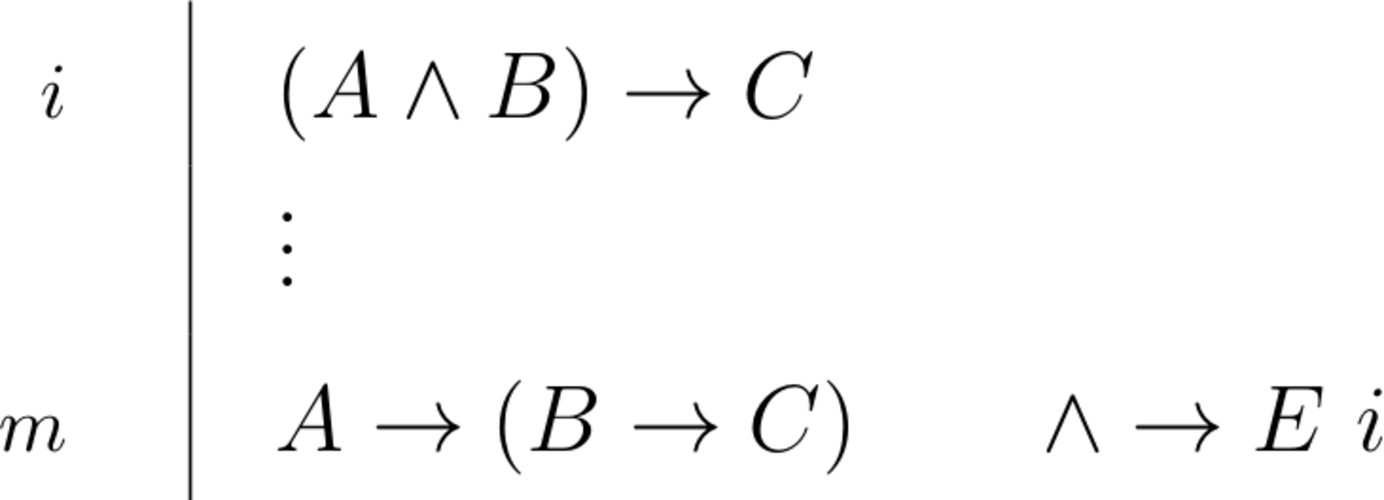\begin{prooftree}\AxiomC{$A \to C, B \to C, \Gamma \vdash D$}\RightLabel{\(\scriptsize{L\lor\to}\)}\UnaryInfC{$(A \lor B) \to C, \Gamma \vdash D$}\end{prooftree}	\begin{prooftree}\AxiomC{$(A \lor B) \to C$}\RightLabel{\scriptsize{$\lor\to E$}}\UnaryInfC{$(A \to C)$}\end{prooftree} \begin{prooftree}\AxiomC{$(A \lor B) \to C$}\RightLabel{\scriptsize{$\lor\to E$}}\UnaryInfC{$(B\to C)$}\end{prooftree}
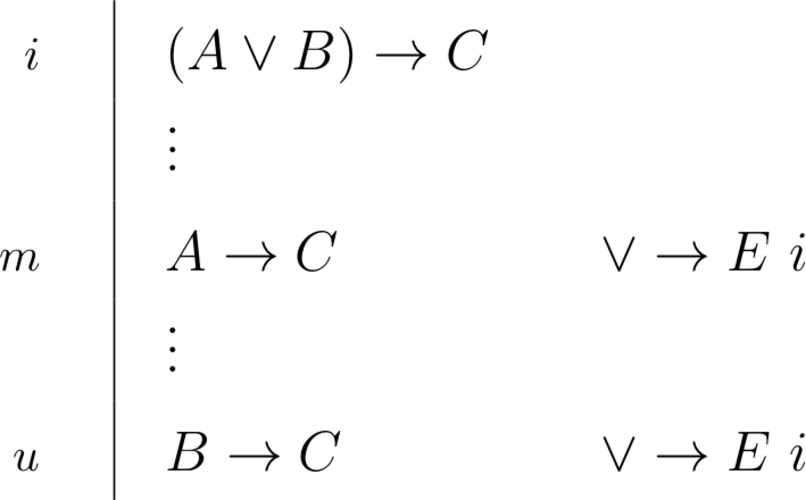\begin{prooftree}\AxiomC{$A, B \to C,\Gamma \vdash B$}\AxiomC{$C,\Gamma \vdash D$}\RightLabel{\(\scriptsize{L\to\to}\)}\BinaryInfC{$(A \to B) \to C, \Gamma \vdash D$}\end{prooftree}	\begin{prooftree}\AxiomC{$(A \to B) \to C$}\RightLabel{\scriptsize{$\to\to E$}}\UnaryInfC{$B \to C$}\end{prooftree}
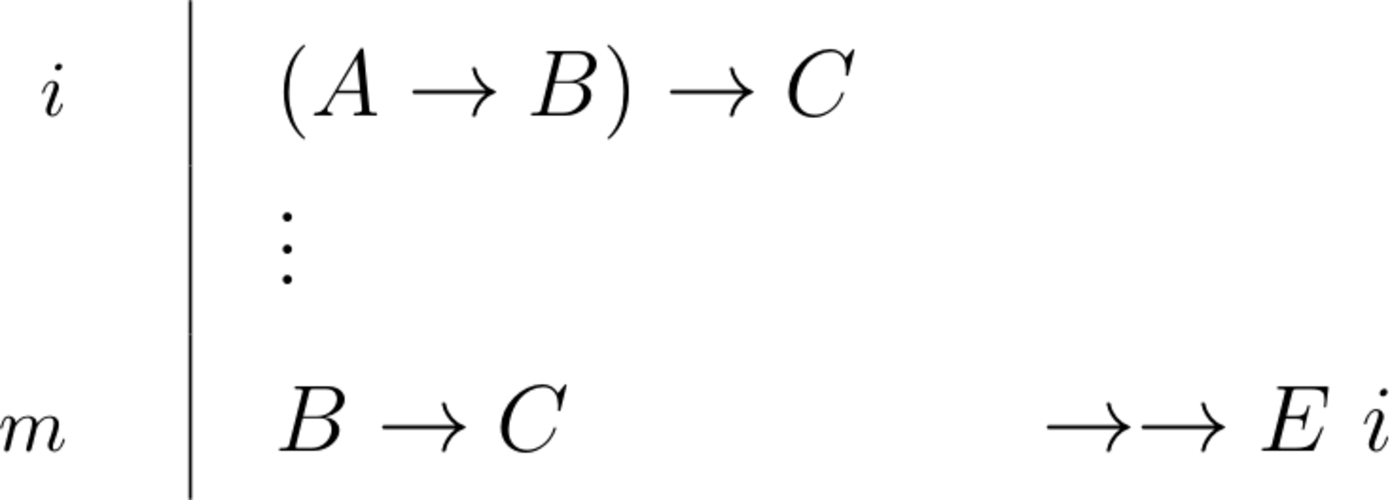\begin{prooftree}\AxiomC{$(A \to B) \to B, \Gamma \vdash B$}\RightLabel{\scriptsize{\(DNE_{m}\)}}\UnaryInfC{$A , \Gamma \vdash B$}\end{prooftree}	\begin{prooftree}\AxiomC{\scriptsize{$i$}}\noLine \UnaryInfC{$(A \to B) \to B$}\noLine\UnaryInfC{$\vdots$}\noLine\UnaryInfC{$B$}\RightLabel{\scriptsize{\(DNE_{m}\)}~\(i\)}\UnaryInfC{$A \to B$}\end{prooftree}
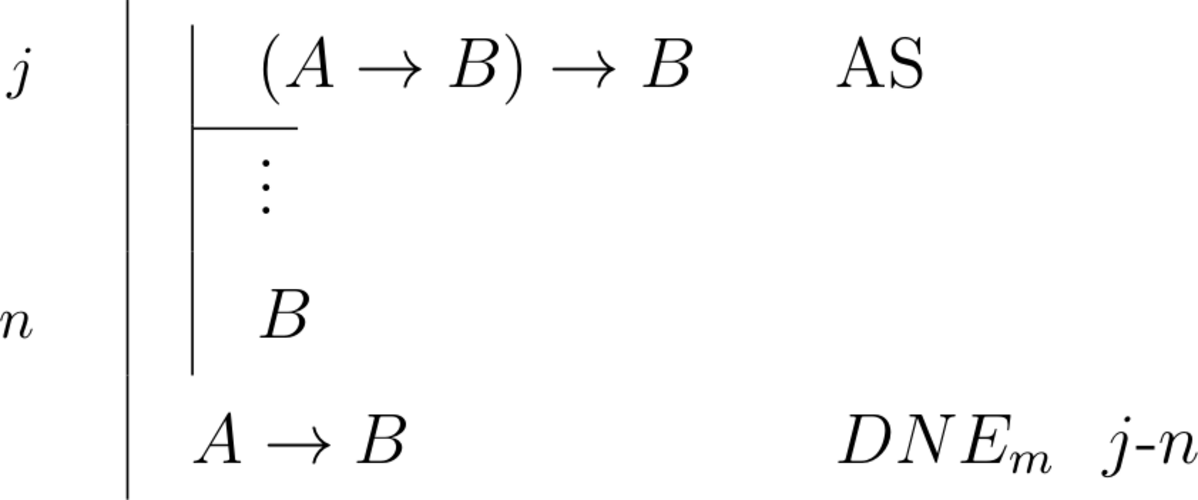\begin{prooftree}\AxiomC{$A, B, \Gamma \vdash C$}\RightLabel{\scriptsize{$L\land$}} \UnaryInfC{$A \land B, \Gamma \vdash C$}\end{prooftree}	\begin{prooftree}\AxiomC{$A \land B$}\RightLabel{\scriptsize{$\land E$}} \UnaryInfC{$A$} \end{prooftree} \begin{prooftree}\AxiomC{$A \land B$}\RightLabel{\scriptsize{$\land E$}} \UnaryInfC{$B$}\end{prooftree}
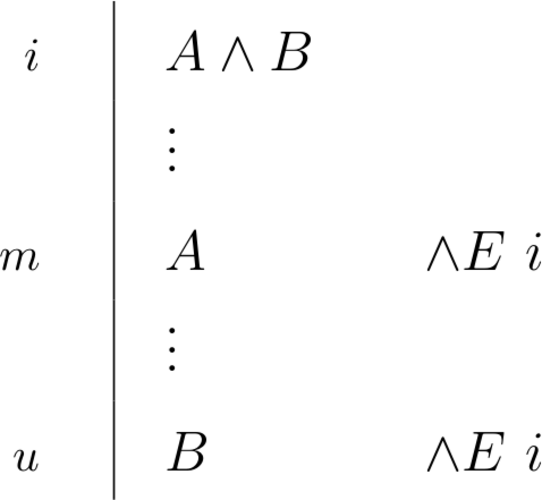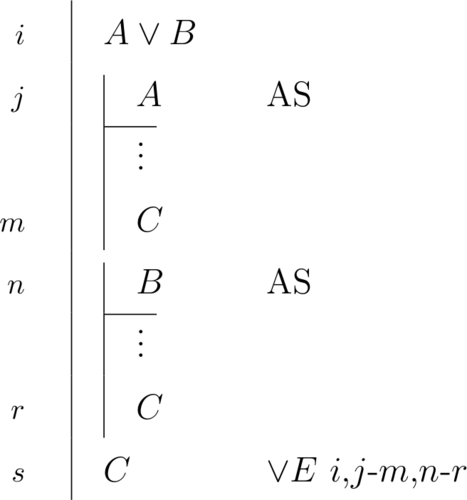
\begin{prooftree}\AxiomC{$A, \Gamma \vdash C$}\AxiomC{$B, \Gamma \vdash C$}\RightLabel{\scriptsize{$L\lor$}}\BinaryInfC{$A \lor B, \Gamma \vdash C$}\end{prooftree}	\begin{prooftree}\AxiomC{$A \lor B$}\AxiomC{\scriptsize{1}}\noLine\UnaryInfC{$A$}\noLine\UnaryInfC{$\vdots$}\noLine\UnaryInfC{$C$}\AxiomC{\scriptsize{2}}\noLine\UnaryInfC{$B$}\noLine\UnaryInfC{$\vdots$}\noLine\UnaryInfC{$C$}\RightLabel{\scriptsize{$\lor E$ 1,2}}\TrinaryInfC{$C$}\end{prooftree}
\begin{prooftree}\AxiomC{$A, \Gamma \vdash B$}\RightLabel{\scriptsize{$R\to$}}\UnaryInfC{$\Gamma \vdash A \to B$}\end{prooftree}	\begin{prooftree}\AxiomC{\scriptsize{1}}\noLine\UnaryInfC{$A$} \noLine\UnaryInfC{$\vdots$}\noLine\UnaryInfC{$B$}\RightLabel{\scriptsize{$\to I$ 1}}\UnaryInfC{$A \to B$}\end{prooftree}
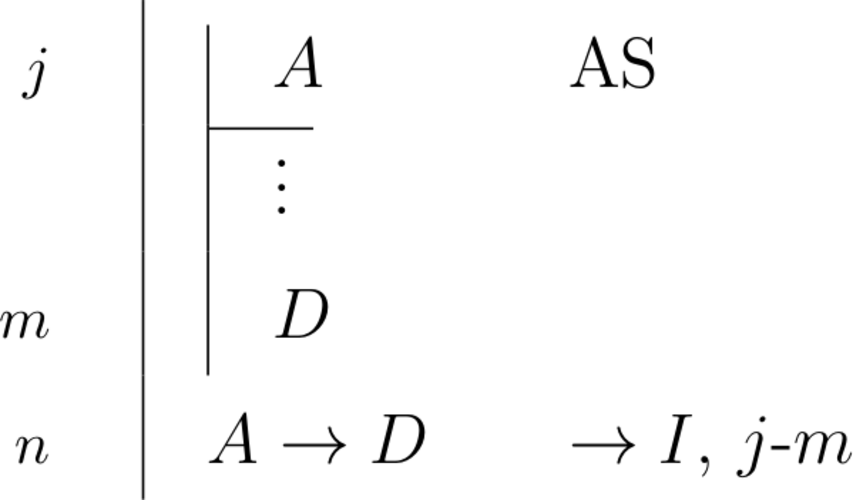\begin{prooftree}\AxiomC{$\Gamma \vdash A$}\AxiomC{$\Gamma \vdash B$}\RightLabel{\scriptsize{$R\land$}}\BinaryInfC{$\Gamma \vdash A \land B$}\end{prooftree}	\begin{prooftree}\AxiomC{$A$}\AxiomC{$B$}\RightLabel{\scriptsize{$\land I$}}\BinaryInfC{$A \land B$}\end{prooftree}
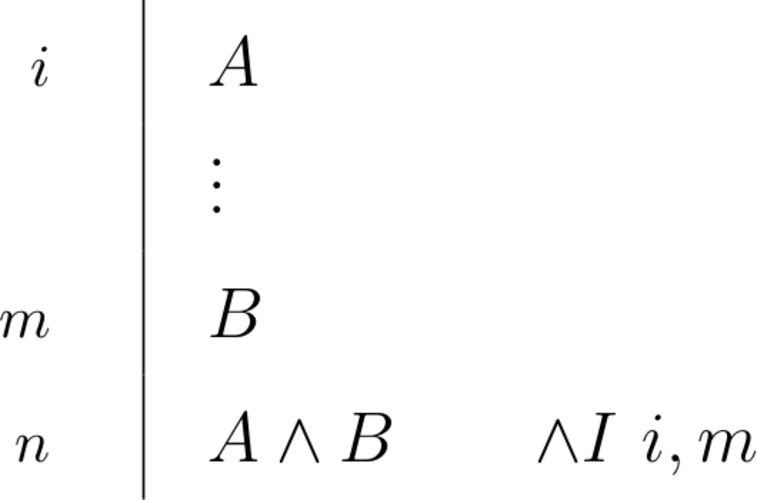\begin{prooftree}\AxiomC{$\Gamma \vdash A$}\RightLabel{\scriptsize{$R\lor$}}\UnaryInfC{$\Gamma \vdash A \lor B$}\end{prooftree}\begin{prooftree} \AxiomC{$\Gamma \vdash B$}\RightLabel{\scriptsize{$R\lor$}}\UnaryInfC{$\Gamma \vdash A \lor B$}\end{prooftree}	\begin{prooftree}\AxiomC{$A$}\RightLabel{\scriptsize{$\lor I$}}\UnaryInfC{$A \lor B$}\end{prooftree} \begin{prooftree}\AxiomC{$B$}\RightLabel{\scriptsize{$\lor I$}}\UnaryInfC{$A \lor B$}\end{prooftree}
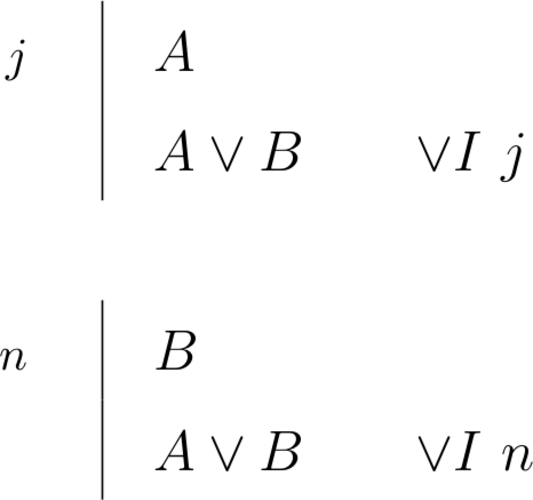\begin{prooftree}\AxiomC{}\RightLabel{\scriptsize{$L\bot$}}\UnaryInfC{$\bot, \Gamma \vdash C$}\end{prooftree}	\begin{prooftree}\AxiomC{$\bot$}\RightLabel{\scriptsize{$\bot E$}}\UnaryInfC{$C$}\end{prooftree}
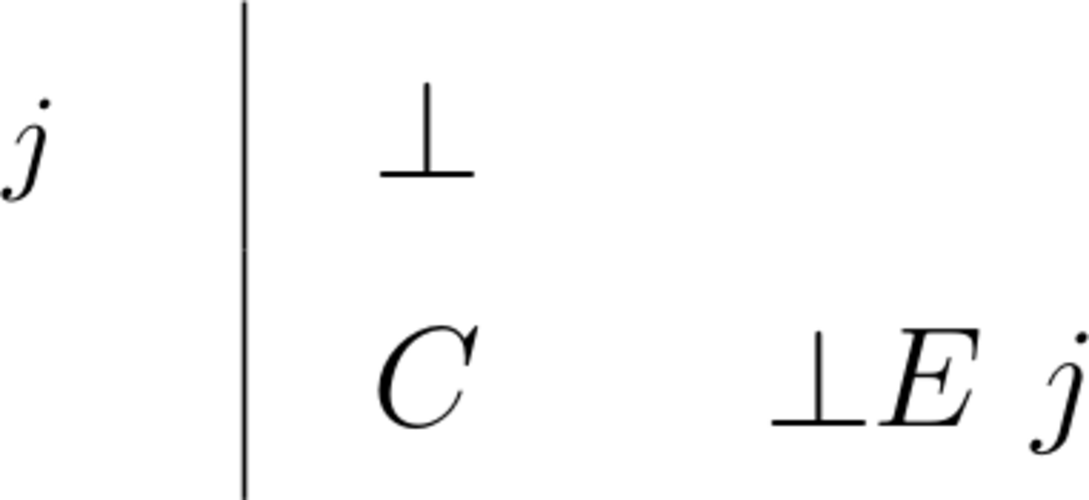\begin{prooftree}\AxiomC{$\lnot A, \Gamma \vdash \bot$}\RightLabel{\scriptsize{$IP$}}\UnaryInfC{$\Gamma \vdash A$}\end{prooftree}	\begin{prooftree}\AxiomC{\scriptsize{1}}\noLine\UnaryInfC{$\lnot A$}\noLine\UnaryInfC{$\vdots$}\noLine\UnaryInfC{$\bot$}\RightLabel{\scriptsize{$IP$ 1}}\UnaryInfC{$A$}\end{prooftree}
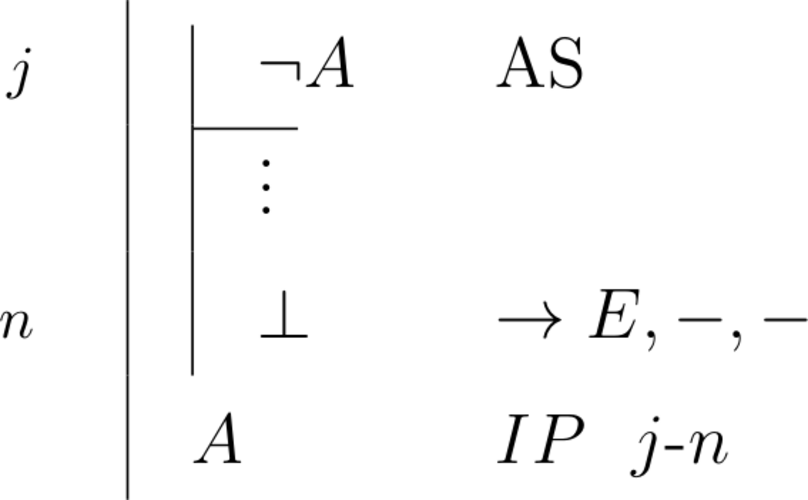\begin{prooftree} \AxiomC{$ Ftt, \forall x Fxx ,\Gamma \vdash C $}\RightLabel{\scriptsize{$ L\forall $}}\UnaryInfC{$ \forall x Fxx, \Gamma \vdash C$}\end{prooftree}	\begin{prooftree}\AxiomC{$\forall x Fxx$}\RightLabel{\scriptsize{$\forall E$}}\UnaryInfC{$Ftt$}\end{prooftree}
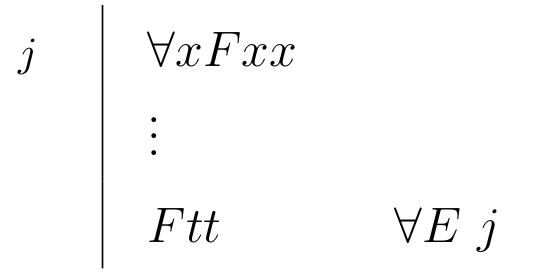\begin{prooftree}\AxiomC{$ \Gamma \vdash Ftt $}\RightLabel{\scriptsize{$ R\exists $}}\UnaryInfC{$\Gamma \vdash \exists y Fyt$}\end{prooftree}	\begin{prooftree}\AxiomC{$ Ftt $}\RightLabel{\scriptsize{$\exists I$}}\UnaryInfC{$\exists y Fyt$}\end{prooftree}
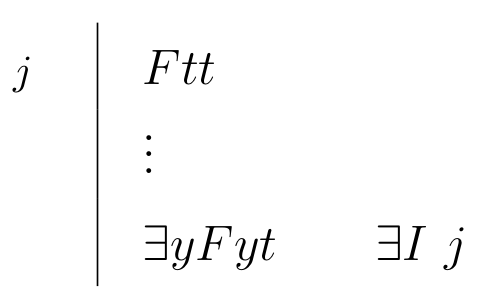\begin{prooftree}\AxiomC{$ \Gamma \vdash Fa $}\RightLabel{\scriptsize{$ R \forall $}}\UnaryInfC{$ \Gamma \vdash \forall x Fx $}\noLine\UnaryInfC{\(a\) = \textit{eigenvariable}} \end{prooftree}	\begin{prooftree}\AxiomC{$Fa$} \RightLabel{\scriptsize{$ \forall I $}}\UnaryInfC{$ \forall x Fx $}\noLine\UnaryInfC{\(a\) = \textit{eigenvariable}}\end{prooftree}
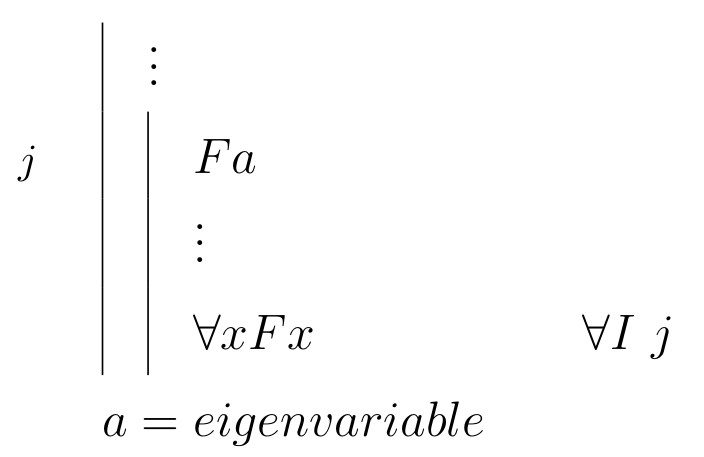\begin{prooftree}\AxiomC{$ Fa, \Gamma \vdash C$}\RightLabel{\scriptsize{$ L \exists $}}\UnaryInfC{$ \exists x Ax, \Gamma \vdash C $} \noLine\UnaryInfC{\(a\) = \textit{eigenvariable}}\end{prooftree}	\begin{prooftree}\AxiomC{$ \exists x Fx $}\AxiomC{\scriptsize{$ i $}} \noLine \UnaryInfC{$ Fa $} \noLine \UnaryInfC{$ \vdots $} \noLine \UnaryInfC{$ G $} \RightLabel{\scriptsize{$ \exists E ~ i $}} \BinaryInfC{$ G $} \noLine\UnaryInfC{\(a\) = \textit{eigenvariable}}\end{prooftree}
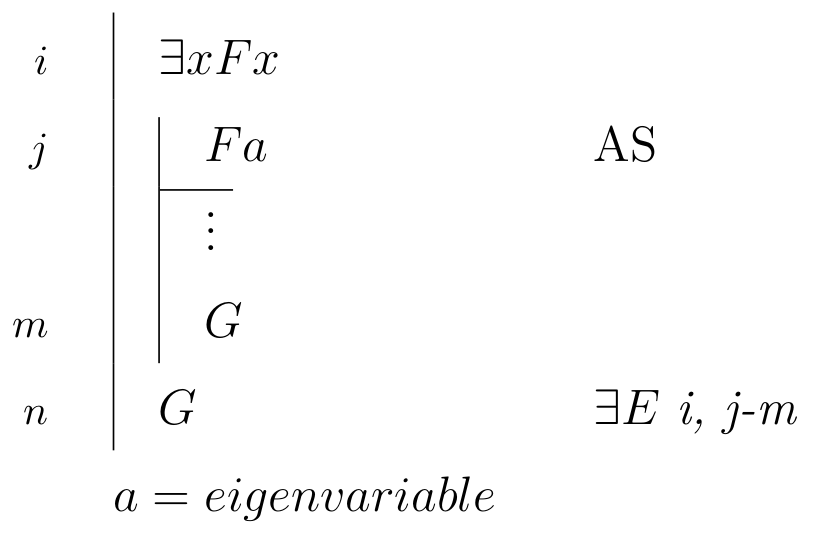\begin{prooftree}\AxiomC{$ \exists x (Fx \to P), \Gamma \vdash D $}\RightLabel{\scriptsize{\(CQ_{c}\)}}\UnaryInfC{$\forall x Fx \to P, \Gamma \vdash D $}\end{prooftree}	\begin{prooftree}\AxiomC{$ \forall x Fx \to P $} \RightLabel{\scriptsize{\(CQ_{c}\)}}\UnaryInfC{$ \exists x(Fx \to P) $}\end{prooftree}
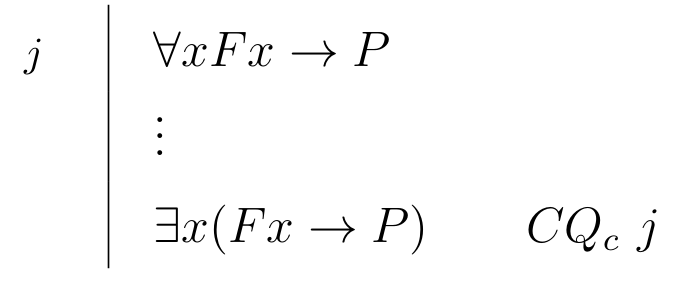\begin{prooftree}\AxiomC{$ \forall x (Fx \to P), \Gamma \vdash D $}\RightLabel{\scriptsize{\(CQ_{m}\)}}\UnaryInfC{$\exists x Fx \to P, \Gamma \vdash D $} \end{prooftree}	\begin{prooftree}\AxiomC{$ \exists x Fx \to P $} \RightLabel{\scriptsize{\(CQ_{m}\)}}\UnaryInfC{$ \forall x(Fx \to P) $}\end{prooftree}
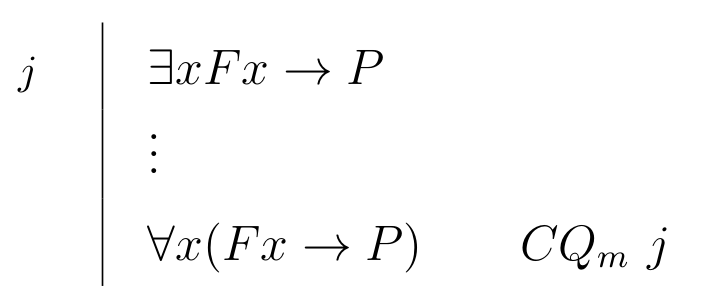